Reproducing Nate Silver's regression analysis on COVID death rates
⋅ 11 minute read
I spent some time recently studying causal inference methods. Two great resources for this are:
- Causal Inference for The Brave and True (frequentist view)
- Statistical Rethinking (Bayesian view).
When I learn about an unfamiliar topic, I will always try to look for real-world examples. In this case I keep my eyes open about articles sharing statistical findings, where I can attempt to reproduce the results.
In Nate Silver’s recent article Fine, I’ll run a regression analysis. But it won’t make you happy he shows the effect of state partisanship and COVID vaccination rates on COVID death rates. The models used are simple linear regressions with one to three independent variables (partisanship, age, vaccination rates).
Silver’s point in the article is only partially about his finding that state partisanship is a good predictor for COVID death rates in that state. Instead, he tries to dismiss critics that argue that simple models are not valid when they leave out additional variables, e.g. age, co-morbidities. While he agrees that one has to justify a particular model design, simple models can deliver true insights while standing up to scrutiny. Moreover he adds that “there’s a general tendency [in the profession] to overfit models.”
This post is not about Silver’s point or the political aspect of the result. I simply wanted to reproduce the findings in the article.
In his article Silver runs four linear regressions:
- impact of state partisanship on COVID death rates
- impact of state partisanship and state age on COVID death rates
- impact of state partisanship, state age, and state vaccination rates on COVID death rates
- impact of state age and state vaccination rates on COVID death rates
We need to collect data for every US state on partisanship, age structure, vaccination rates, and COVID death rates. It turned out, perhaps not surprisingly, that finding and assembling the dataset from open sources took significantly more time than setting up the regressions. I had three issues when I tried to assemble the data from the sources that the article links to:
- one source didn’t allow me to download the data as a file and I didn’t want to scrape or copy-paste from the website
- one source didn’t allow me to view the data on the same reference day as in the article
- one source didn’t provide the data as a file for free
So I had to use in some cases different sources.
Building the data set
We are building the data set from four sources:
- US states COVID cases and deaths: https://github.com/nytimes/covid-19-data/blob/62ef34cfcb60214be873a38d73619da9ea57d50b/us-states.csv
- US states age statistics: https://www.prb.org/resources/which-us-states-are-the-oldest/
- US states vaccination rates: ourworldindata.org (archive.org version)
- US states election results 2020: https://www.kaggle.com/code/paultimothymooney/2020-usa-election-vote-percentages-by-state/output
COVID death rates
We want to calculate the COVID death rates (COVID deaths per 1M population) between two points in time (1. February 2021 when vaccines became widely available and 23. March 2023 as in the article). Silver links to worldometer.info as his dataset for covid deaths per state. However, I couldn’t find a way to download the data in timeseries form (numbers for each day) without scraping the website. Instead we are using the equivalent numbers published by the New York Times. Let’s load the CSV file into a pandas dataframe:
import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
df = pd.read_csv("us-states.csv")
df['date'] = pd.to_datetime(df['date'])
# create two series for the two dates of interest and rename the columns
deaths_february = df[df.date == '2021-02-01'][["state", "deaths"]].rename(columns = {"deaths" : "deaths_2021_02_01"})
deaths_last = df[df.date == '2023-03-23'][["state", "deaths"]].rename(columns = {"deaths" : "deaths_2023_03_23"})
With the two pandas series deaths_february and deaths_last we can calculate the number of death in this time period.
deaths = deaths_last.merge(deaths_february, how = 'left', on = 'state').dropna(axis = 'index')
deaths["deaths_after_vaccine"] = deaths["deaths_2023_03_23"] - deaths["deaths_2021_02_01"]
Now we can look at the state numbers for COVID deaths between 01.02.2021 and 23.03.2023:
deaths
| state | deaths_2023_03_23 | deaths_2021_02_01 | deaths_after_vaccine | |
|---|---|---|---|---|
| 0 | Alabama | 21631 | 7688.0 | 13943.0 |
| 1 | Alaska | 1438 | 253.0 | 1185.0 |
| 3 | Arizona | 33190 | 13124.0 | 20066.0 |
| 4 | Arkansas | 13068 | 4895.0 | 8173.0 |
| 5 | California | 104277 | 41284.0 | 62993.0 |
| 6 | Colorado | 14245 | 5737.0 | 8508.0 |
| 7 | Connecticut | 12270 | 7119.0 | 5151.0 |
| 8 | Delaware | 3352 | 1101.0 | 2251.0 |
| 9 | District of Columbia | 1432 | 916.0 | 516.0 |
| 10 | Florida | 87141 | 26684.0 | 60457.0 |
| 11 | Georgia | 41055 | 13821.0 | 27234.0 |
| 12 | Guam | 416 | 130.0 | 286.0 |
| 13 | Hawaii | 1851 | 407.0 | 1444.0 |
| 14 | Idaho | 5456 | 1737.0 | 3719.0 |
| 15 | Illinois | 41618 | 21273.0 | 20345.0 |
| 16 | Indiana | 26179 | 9989.0 | 16190.0 |
| 17 | Iowa | 10770 | 4906.0 | 5864.0 |
| 18 | Kansas | 10232 | 3809.0 | 6423.0 |
| 19 | Kentucky | 18348 | 3995.0 | 14353.0 |
| 20 | Louisiana | 18835 | 8912.0 | 9923.0 |
| 21 | Maine | 2981 | 595.0 | 2386.0 |
| 22 | Maryland | 16672 | 7154.0 | 9518.0 |
| 23 | Massachusetts | 24441 | 14607.0 | 9834.0 |
| 24 | Michigan | 42311 | 15527.0 | 26784.0 |
| 25 | Minnesota | 14964 | 6270.0 | 8694.0 |
| 26 | Mississippi | 13431 | 6056.0 | 7375.0 |
| 27 | Missouri | 23998 | 7182.0 | 16816.0 |
| 28 | Montana | 3701 | 1235.0 | 2466.0 |
| 29 | Nebraska | 5068 | 2031.0 | 3037.0 |
| 30 | Nevada | 12093 | 4281.0 | 7812.0 |
| 31 | New Hampshire | 3018 | 1059.0 | 1959.0 |
| 32 | New Jersey | 36097 | 21513.0 | 14584.0 |
| 33 | New Mexico | 9110 | 3297.0 | 5813.0 |
| 34 | New York | 80109 | 43354.0 | 36755.0 |
| 35 | North Carolina | 29746 | 9397.0 | 20349.0 |
| 36 | North Dakota | 2529 | 1447.0 | 1082.0 |
| 37 | Northern Mariana Islands | 41 | 2.0 | 39.0 |
| 38 | Ohio | 42061 | 11233.0 | 30828.0 |
| 39 | Oklahoma | 16549 | 3564.0 | 12985.0 |
| 40 | Oregon | 9451 | 1980.0 | 7471.0 |
| 41 | Pennsylvania | 50701 | 21741.0 | 28960.0 |
| 42 | Puerto Rico | 5848 | 1836.0 | 4012.0 |
| 43 | Rhode Island | 3915 | 2173.0 | 1742.0 |
| 44 | South Carolina | 20192 | 7283.0 | 12909.0 |
| 45 | South Dakota | 3222 | 1778.0 | 1444.0 |
| 46 | Tennessee | 29035 | 9660.0 | 19375.0 |
| 47 | Texas | 94518 | 37405.0 | 57113.0 |
| 48 | Utah | 5316 | 1669.0 | 3647.0 |
| 49 | Vermont | 939 | 175.0 | 764.0 |
| 50 | Virgin Islands | 130 | 24.0 | 106.0 |
| 51 | Virginia | 23782 | 6474.0 | 17308.0 |
| 52 | Washington | 15905 | 4404.0 | 11501.0 |
| 53 | West Virginia | 8132 | 2028.0 | 6104.0 |
| 54 | Wisconsin | 16485 | 6439.0 | 10046.0 |
| 55 | Wyoming | 2014 | 596.0 | 1418.0 |
Age characteristics
We load data for US states population age characteristics and calculate the proportion of the state population equal or older than 65. We would expect that states with an older population are more severely affected by COVID (all else being equal).
states_population = pd.read_csv("states_population_age_2020.csv", thousands=',').drop(["Rank", "Population Ages 65+ (percent of state population)"], axis = 1)
states_population = states_population.rename(columns = {"State" : "state", "Total Resident Population (thousands)": "total_population_thousands", "Population Ages 65+ (thousands)" : "population_age65_thousands"})
states_population["perc_over_65"] = states_population["population_age65_thousands"] / states_population["total_population_thousands"] * 100.0
Next we add the perc_over_65 column to the deaths dataframe.
# drop due to missing population data for DC, Guam, Puerto Rico, Northern Mariana Islands, Virgin Islands
deaths_and_states = deaths.merge(states_population[["state", "total_population_thousands", "perc_over_65"]], on = 'state', how = 'left').dropna()
Moreover, to use the same variable scaling as in the article, we scale the deaths_after_vaccine variable from absolute numbers to be COVID deaths per million population.
deaths_and_states["deaths_per_million"] = deaths_and_states["deaths_after_vaccine"] / ((deaths_and_states["total_population_thousands"] * 1000) / 1_000_000 )
# dataframe with deaths, population, and age variable
deaths_and_states.head(5)
| state | deaths_2023_03_23 | deaths_2021_02_01 | deaths_after_vaccine | total_population_thousands | perc_over_65 | deaths_per_million | |
|---|---|---|---|---|---|---|---|
| 0 | Alabama | 21631 | 7688.0 | 13943.0 | 4922.0 | 17.757009 | 2832.791548 |
| 1 | Alaska | 1438 | 253.0 | 1185.0 | 731.0 | 13.132695 | 1621.067031 |
| 2 | Arizona | 33190 | 13124.0 | 20066.0 | 7421.0 | 18.515025 | 2703.948255 |
| 3 | Arkansas | 13068 | 4895.0 | 8173.0 | 3031.0 | 17.683933 | 2696.469812 |
| 4 | California | 104277 | 41284.0 | 62993.0 | 39368.0 | 15.179841 | 1600.106686 |
Presidential election results
Similar to the article we want to generate a variable biden which indicates Joe Biden’s margin of victory over Donald Trump in the 2020 elections.
# load election results by state for 2020 presidential election
election_results = pd.read_csv("democratic_vs_republican_votes_by_usa_state_2020.csv").drop("usa_state_code", axis = 1)
election_results["biden"] = election_results["percent_democrat"] - 50
election_results.head(10)
| state | DEM | REP | usa_state | percent_democrat | biden | |
|---|---|---|---|---|---|---|
| 0 | Alabama | 843473 | 1434159 | Alabama | 37.032892 | -12.967108 |
| 1 | Alaska | 45758 | 80999 | Alaska | 36.098993 | -13.901007 |
| 2 | Arizona | 1643664 | 1626679 | Arizona | 50.259682 | 0.259682 |
| 3 | Arkansas | 420985 | 761251 | Arkansas | 35.609218 | -14.390782 |
| 4 | California | 9315259 | 4812735 | California | 65.934760 | 15.934760 |
| 5 | Colorado | 1753416 | 1335253 | Colorado | 56.769307 | 6.769307 |
| 6 | Connecticut | 1059252 | 699079 | Connecticut | 60.241900 | 10.241900 |
| 7 | Delaware | 295413 | 199857 | Delaware | 59.646859 | 9.646859 |
| 8 | District of Columbia | 258561 | 14449 | District of Columbia | 94.707520 | 44.707520 |
| 9 | Florida | 5294767 | 5667834 | Florida | 48.298456 | -1.701544 |
# merge to deaths dataframe
death_and_election = deaths_and_states.merge(election_results[["state", "biden"]], how = "left", on = 'state')
Vaccination rates
Lastly, we add the vaccination rates per state after the pandemic was over. I use the vaccination rates from 10.5.2023 as this data was easily available.
vaccinations_raw = pd.read_csv("us_state_vaccinations.csv").rename(columns={"location": "state"})
vaccinations_raw.replace({'New York State': 'New York'}, inplace=True)
# chose date and relevant columns
vaccinations = vaccinations_raw[vaccinations_raw.date == '2023-05-10'][["state","people_vaccinated_per_hundred"]]
Next, we merge the vaccination rates with the dataframe to get our final dataset.
dataset = death_and_election.merge(vaccinations, how = "left", on = 'state')
dataset[["state", "deaths_per_million", "biden", "perc_over_65", "people_vaccinated_per_hundred"]].head(5)
| state | deaths_per_million | biden | perc_over_65 | people_vaccinated_per_hundred | |
|---|---|---|---|---|---|
| 0 | Alabama | 2832.791548 | -12.967108 | 17.757009 | 65.12 |
| 1 | Alaska | 1621.067031 | -13.901007 | 13.132695 | 73.23 |
| 2 | Arizona | 2703.948255 | 0.259682 | 18.515025 | 78.37 |
| 3 | Arkansas | 2696.469812 | -14.390782 | 17.683933 | 70.09 |
| 4 | California | 1600.106686 | 15.934760 | 15.179841 | 85.07 |
I am also storing the final dataset as a parquet file in case you want to play with it. To find it, follow the link at the bottom of the page.
dataset[["state", "deaths_per_million", "biden", "perc_over_65", "people_vaccinated_per_hundred"]].to_parquet("death_partisanship_final_dataset.parquet", engine = 'pyarrow')
Regressions
With the assembled dataset we can now reproduce Nate Silver’s findings.
1. Regression: state partisanship on death rates
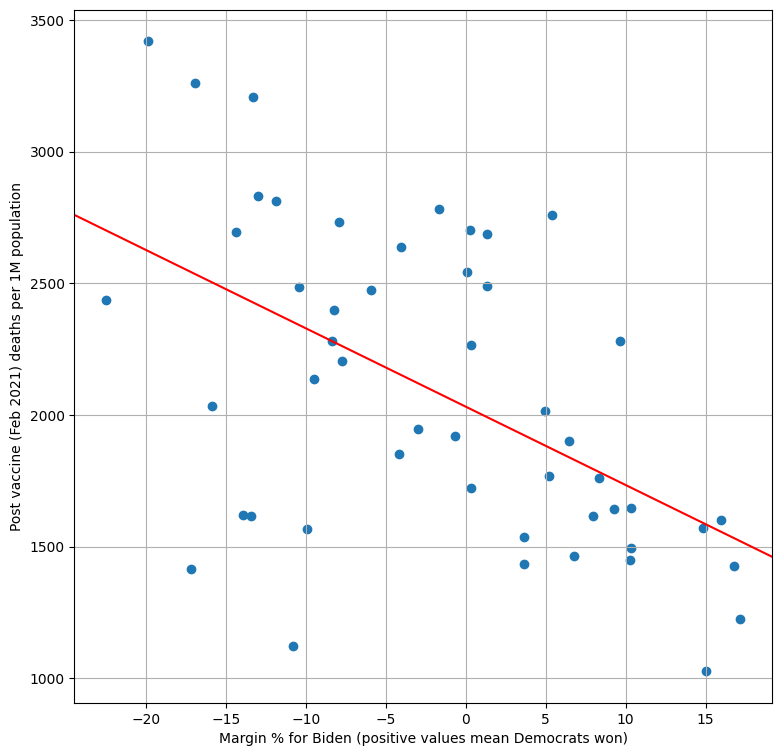
Silver starts with a one-variable baseline model. And indeed biden, Joe Biden’s winning margin, is a statistically significant predictor of COVID deaths. According to the model, one percentage point increase in Biden’s margin reduced expected COVID deaths by ~30 covid deaths per million population.
x = dataset[['biden']]
y = dataset['deaths_per_million']
# add a constant term to the model
x = sm.add_constant(x)
# run regression
model = sm.OLS(y, x).fit()
print_model = model.summary()
print(print_model)
OLS Regression Results
==============================================================================
Dep. Variable: deaths_per_million R-squared: 0.286
Model: OLS Adj. R-squared: 0.272
Method: Least Squares F-statistic: 19.27
Date: Sun, 14 Jan 2024 Prob (F-statistic): 6.22e-05
Time: 18:05:09 Log-Likelihood: -381.14
No. Observations: 50 AIC: 766.3
Df Residuals: 48 BIC: 770.1
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 2031.3050 72.204 28.133 0.000 1886.129 2176.481
biden -29.7773 6.784 -4.389 0.000 -43.418 -16.137
==============================================================================
Omnibus: 0.718 Durbin-Watson: 2.263
Prob(Omnibus): 0.698 Jarque-Bera (JB): 0.732
Skew: -0.266 Prob(JB): 0.694
Kurtosis: 2.737 Cond. No. 10.8
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
We can also plot the data set and the regression line to get a more intuitive overview of the result:
fig, ax = plt.subplots(figsize = (9, 9))
ax.scatter(dataset["biden"], dataset["deaths_per_million"])
plt.xlabel("Margin % for Biden (positive values mean Democrats won)")
plt.ylabel("Post vaccine (Feb 2021) deaths per 1M population")
b, m = model.params
ax.axline(xy1=(0, b), slope=m, color='red')
plt.grid()
2. Regression: state partisanship and age on death rates
Silver’s article is a response to criticism that the model above is not valuable because different states have different age structures and that may explain most of the variation in death rates. Silver remarks that the results hold even when controlling for age. We can add age perc_over_65 to the model and re-run the regression and indeed we get the same result. biden is still significant with a similar coefficient.
x2 = dataset[['biden', 'perc_over_65']]
y2 = dataset['deaths_per_million']
x2 = sm.add_constant(x2)
model2 = sm.OLS(y2, x2).fit()
print_model2 = model2.summary()
print(print_model2)
OLS Regression Results
==============================================================================
Dep. Variable: deaths_per_million R-squared: 0.397
Model: OLS Adj. R-squared: 0.371
Method: Least Squares F-statistic: 15.44
Date: Sun, 14 Jan 2024 Prob (F-statistic): 6.99e-06
Time: 18:05:12 Log-Likelihood: -376.95
No. Observations: 50 AIC: 759.9
Df Residuals: 47 BIC: 765.6
Df Model: 2
Covariance Type: nonrobust
================================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------
const 256.0210 609.788 0.420 0.677 -970.714 1482.756
biden -32.9481 6.397 -5.151 0.000 -45.817 -20.079
perc_over_65 101.6118 34.690 2.929 0.005 31.824 171.400
==============================================================================
Omnibus: 1.194 Durbin-Watson: 2.318
Prob(Omnibus): 0.551 Jarque-Bera (JB): 1.061
Skew: -0.162 Prob(JB): 0.588
Kurtosis: 2.365 Cond. No. 162.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
3. Regression: state partisanship, age, and vaccination rates on death rates
Clearly your political leanings are not a predictor for your chance of dying from COVID. The assumption behind the model is that Republicans have been less likely to get vaccinated, and unvaccinated humans have a higher mortality w.r.t COVID. We can check what happens if we add the vaccination rates as a variable to the model.
We can see below that vaccination rate is significant and explains away the effect of the biden variable.
x3 = dataset[['biden', 'perc_over_65', 'people_vaccinated_per_hundred']]
y3 = dataset['deaths_per_million']
x3 = sm.add_constant(x3)
model3 = sm.OLS(y3, x3).fit()
print_model3 = model3.summary()
print(print_model3)
OLS Regression Results
==============================================================================
Dep. Variable: deaths_per_million R-squared: 0.450
Model: OLS Adj. R-squared: 0.414
Method: Least Squares F-statistic: 12.55
Date: Sun, 14 Jan 2024 Prob (F-statistic): 4.01e-06
Time: 18:05:13 Log-Likelihood: -374.63
No. Observations: 50 AIC: 757.3
Df Residuals: 46 BIC: 764.9
Df Model: 3
Covariance Type: nonrobust
=================================================================================================
coef std err t P>|t| [0.025 0.975]
-------------------------------------------------------------------------------------------------
const 1528.3900 841.133 1.817 0.076 -164.723 3221.503
biden -15.9990 10.110 -1.583 0.120 -36.349 4.351
perc_over_65 114.7298 34.042 3.370 0.002 46.207 183.253
people_vaccinated_per_hundred -18.5072 8.743 -2.117 0.040 -36.106 -0.908
==============================================================================
Omnibus: 0.262 Durbin-Watson: 2.192
Prob(Omnibus): 0.877 Jarque-Bera (JB): 0.454
Skew: 0.027 Prob(JB): 0.797
Kurtosis: 2.537 Cond. No. 1.08e+03
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1.08e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
4. Regression: age and vaccination rates on death rates
In a final step, we remove the correlated variable biden from the model to demonstrate the impact of age and vaccination rate on death rate:
x4 = dataset[['perc_over_65', 'people_vaccinated_per_hundred']]
y4 = dataset['deaths_per_million']
x4 = sm.add_constant(x4)
model4 = sm.OLS(y4, x4).fit()
print_model4 = model4.summary()
print(print_model4)
OLS Regression Results
==============================================================================
Dep. Variable: deaths_per_million R-squared: 0.420
Model: OLS Adj. R-squared: 0.396
Method: Least Squares F-statistic: 17.03
Date: Sun, 14 Jan 2024 Prob (F-statistic): 2.74e-06
Time: 18:05:14 Log-Likelihood: -375.95
No. Observations: 50 AIC: 757.9
Df Residuals: 47 BIC: 763.6
Df Model: 2
Covariance Type: nonrobust
=================================================================================================
coef std err t P>|t| [0.025 0.975]
-------------------------------------------------------------------------------------------------
const 2386.5532 653.203 3.654 0.001 1072.478 3700.629
perc_over_65 117.0242 34.551 3.387 0.001 47.516 186.532
people_vaccinated_per_hundred -29.4653 5.423 -5.434 0.000 -40.374 -18.556
==============================================================================
Omnibus: 0.653 Durbin-Watson: 2.211
Prob(Omnibus): 0.722 Jarque-Bera (JB): 0.527
Skew: 0.244 Prob(JB): 0.768
Kurtosis: 2.881 Cond. No. 829.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Jupyter Notebook
You can find the jupyter notebook and the datasets for this post here .
If you have any thoughts, questions, or feedback about this post, I would love to hear it. Please reach out to me via email.
Tags:#notebook #statistics